POSTS
Lucy's Secret Number Puzzle
A good friend from Slovenia sent me this nice puzzle the other day:
Great riddle, but obviously a bad party if they discussed lucky numbers… J
You are at a party and overhear a conversation between Lucy and her friend.
In the conversation, Lucy mentions she has a secret number between 1 and 100.
She also confesses the following information:
“The number is uniquely describable by the answers to the following four questions:”
Q1) Is the number divisible by two?
Q2) Is the number divisible by three?
Q3) Is the number divisible by five?
Q4) Is the number divisible by seven?
She then proceeds to whisper the answers to these questions to her friend. Unfortunately, because of the ambient noise at the party, you only hear the answer to one of the questions.
However, knowing just this one answer allows you to determine Lucy’s secret number.
- Which question and answer did you overhear?
- If the answer to this question is “Yes”, what is Lucy’s secret number?”
My friend is a Mathematician and I think he managed to find the answer in a couple of minutes probably in his head or by just using pen and paper. Myself however, as a true programmer, I found it more intriguing to describe this problem in Python and let the computer solve it!
I will describe step-by-step how I came up with a solution:
First I decided to make four different sets. Each set corresponds to all the numbers between 1 - 100 that we can get if we answer ‘Yes’ to one of the four questions. These are all the possible numbers contained in every set:
>>> {x for x in range(1, 101) if x % 2 == 0}
{2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36,
38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72,
74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100}>>> {x for x in range(1, 101) if x % 3 == 0}
{3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54,
57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99}>>> {x for x in range(1, 101) if x % 5 == 0}
{5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85,
90, 95, 100}>>> {x for x in range(1, 101) if x % 7 == 0}
{7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98}I group these four sets inside a list container called divisible_sets
- Why sets and not lists?
- Why group them into a list container?
The above questions will be answered later as we describe more the algorithm.
divisible_sets = [{x for x in range(1, 101) if x % 2 == 0},
{x for x in range(1, 101) if x % 3 == 0},
{x for x in range(1, 101) if x % 5 == 0},
{x for x in range(1, 101) if x % 7 == 0}](number IS divisible by TWO, number IS NOT divisible by THREE, number IS divisible by FIVE, number IS NOT divisible by SEVEN).
from itertools import product
for flag in product([0, 1], repeat=4):
print(flag)>>>
(0, 0, 0, 0)
(0, 0, 0, 1)
(0, 0, 1, 0)
(0, 0, 1, 1)
(0, 1, 0, 0)
(0, 1, 0, 1)
(0, 1, 1, 0)
(0, 1, 1, 1)
(1, 0, 0, 0)
(1, 0, 0, 1)
(1, 0, 1, 0)
(1, 0, 1, 1)
(1, 1, 0, 0)
(1, 1, 0, 1)
(1, 1, 1, 0)
(1, 1, 1, 1)Now we can observe that every binary number is actually a flag telling us whether we want to enforce a condition from the precomputed sets or not. For example the number (0, 0, 0, 1) tells us that we want to enforce the following condition:
(number IS NOT divisible by TWO, number IS NOT divisible by THREE, number IS NOT divisible by FIVE, number IS divisible by SEVEN).
The fourth bit corresponds to the fourth set in our collection of sets, same as the position of the bit that is flagged as one. Do you see the pattern? That is the reason why we decided to group the sets in a list, in order to have an indexing that we can later associate with the position of a binary bit.
Now comes the next question:
- Why did we choose sets?
Well there are some really handy and fast set operations that we can use in our case namely set intersection and set difference.
The idea again is to start with the set of all possible numbers which is the set of all numbers between 1 and 100. Then we take one combination of answers which is a 4-bit number and we check all bits from left to right:
-
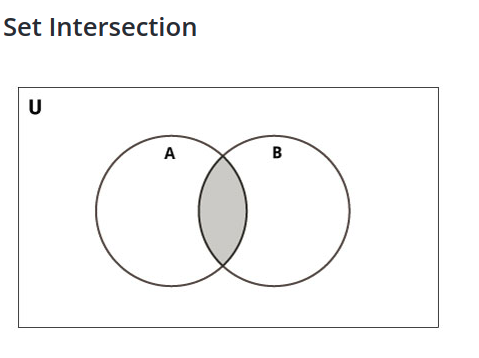
If we find a “1” it means we need to compute the intersection of the set we have with the corresponding set from the divisible_sets
-
If we find a “0” then we need to compute the difference of the set we have with the corresponding set from the divisible_sets
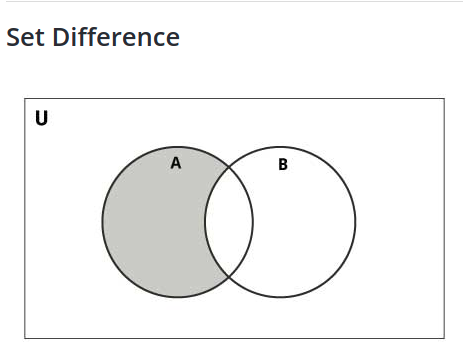 One example: Say our initial set is {2, 3, 4, 5} and we find a “1” as the first binary bit. The first binary bit corresponds to the question “Q1) Is the number divisible by two?” and because it is “1” it corresponds to a “YES” answer. If we follow the algorithm described above we need to find from our initial set all the numbers that are divisible by 2, which are {2, 4} or the intersection of our initial set with {x for x in range(1, 101) if x % 2 == 0}. Similarly if we find “0” as the first binary bit, this would correspond as a “NO” answer to the question. We would then need to find from our initial set all the numbers that are NOT divisible by 2, which are {3, 5} or the difference of our initial set with {x for x in range(1, 101) if x % 2 == 0}.
One example: Say our initial set is {2, 3, 4, 5} and we find a “1” as the first binary bit. The first binary bit corresponds to the question “Q1) Is the number divisible by two?” and because it is “1” it corresponds to a “YES” answer. If we follow the algorithm described above we need to find from our initial set all the numbers that are divisible by 2, which are {2, 4} or the intersection of our initial set with {x for x in range(1, 101) if x % 2 == 0}. Similarly if we find “0” as the first binary bit, this would correspond as a “NO” answer to the question. We would then need to find from our initial set all the numbers that are NOT divisible by 2, which are {3, 5} or the difference of our initial set with {x for x in range(1, 101) if x % 2 == 0}.
The above algorithm can be described in the following lines where we use operator "&" for set intersection and operator "-" for set difference. If we apply all these four conditions to the initial set of 100 numbers we are left with a set containing the numbers for which all these conditions are satisfied.
for flag in product([0, 1], repeat=4):
possible_numbers = set(range(101))
for index, value in enumerate(flag):
if value:
possible_numbers &= divisible_sets[index]
else:
possible_numbers -= divisible_sets[index]
print(flag, sorted(possible_numbers))>>>
(divisible by 2, divisible by 3, divisible by 5, divisible by 7) :
[list of numbers]
(0, 0, 0, 0) : [1, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,
61, 67, 71, 73, 79, 83, 89, 97]
(0, 0, 0, 1) : [7, 49, 77, 91]
(0, 0, 1, 0) : [5, 25, 55, 65, 85, 95]
(0, 0, 1, 1) : [35]
(0, 1, 0, 0) : [3, 9, 27, 33, 39, 51, 57, 69, 81, 87, 93, 99]
(0, 1, 0, 1) : [21, 63]
(0, 1, 1, 0) : [15, 45, 75]
(0, 1, 1, 1) : []
(1, 0, 0, 0) : [2, 4, 8, 16, 22, 26, 32, 34, 38, 44, 46, 52, 58, 62,
64, 68, 74, 76, 82, 86, 88, 92, 94]
(1, 0, 0, 1) : [14, 28, 56, 98]
(1, 0, 1, 0) : [10, 20, 40, 50, 80, 100]
(1, 0, 1, 1) : [70]
(1, 1, 0, 0) : [6, 12, 18, 24, 36, 48, 54, 66, 72, 78, 96]
(1, 1, 0, 1) : [42, 84]
(1, 1, 1, 0) : [30, 60, 90]
(1, 1, 1, 1) : []On the right in the list of numbers you can see which “secret number” could have triggered every answer. As you can see there are combinations that do not correspond to any number between 1 - 100 such as (0, 1, 1, 1) and (1, 1, 1, 1). Notice also that all numbers that correspond to the first condition (0, 0, 0, 0), apart from “1”, are all the prime numbers appearing after the biggest divisor (7) and before the maximum number (100).
Now remember that Lucy said that the answers to the questions uniquely determine her number? This means we should look at all possible combinations that have just one solution. There are only two of them:
>>>
(divisible by 2, divisible by 3, divisible by 5, divisible by 7) :
[list of numbers]
(0, 0, 1, 1) : [35]
(1, 0, 1, 1) : [70]How exciting! We now know that the secret number is either 35 or 70. But we still have one clue to help us. The answer to the secret question was “YES”. So, we need to check which of those two combinations has a unique “YES” condition that we cannot find on the other. To do so we check those tuples index by index to see if we find a unique “1” in any of them. In our case we only have two tuples but since we devise our algorithm beforehand we don’t know that and we try to be as generic as possible. Perhaps there were 10 combinations with only one secret number and we need to check all of them!
In order to check the values of two or more tuples at every index we use the zip built-in method. Here is a small example: Say we want to find the unique “1” bits in the following list of tuples:
tup_to_check = [(0, 0, 0, 1), (1, 0, 1, 0), (0, 0, 1, 0), (1, 0, 0, 0)]Using the zip built-in we can have the tuples of all the values appearing at the same index:
>>> list(zip(*tup_to_check))
[(0, 1, 0, 1), (0, 0, 0, 0), (0, 1, 1, 0), (1, 0, 0, 0)]Now we need to search in these list for tuples containing exactly one 1-bit. We do that using the sum() Python built-in and checking against a sum of 1.
>>> sum((0, 1, 0, 1)) == 1
False
>>> sum((0, 0, 0, 0)) == 1
False
>>> sum((0, 1, 1, 0)) == 1
False
>>> sum((1, 0, 0, 0)) == 1
Trueall_questions = ["Q1) Is the number divisible by two?",
"Q2) Is the number divisible by three?",
"Q3) Is the number divisible by five?",
"Q4) Is the number divisible by seven?"]
def which_question_did_we_hear():
solutions = {35: (0, 0, 1, 1), 70: (1, 0, 1, 1)}
for question_number, tup in enumerate((zip(*solutions.values()))):
if sum(tup) == 1:
return(all_questions[question_number])>>> which_question_did_we_hear()
'Q1) Is the number divisible by two?'And finally let’s find the number we heard!
def what_is_the_secret_number():
solutions = {35: (0, 0, 1, 1), 70: (1, 0, 1, 1)}
question_index = all_questions.index(which_question_did_we_hear())
for number in solutions:
if solutions[number][question_index]:
return number>>> what_is_the_secret_number()
70Indeed 70 is the only number that can be uniquely determined by all these four questions.
Finally here is the whole code that finds the number, only slightly changed and optimized than the step by step presentation we used:
from itertools import product
def find_secret_number():
divisible_sets = [{x for x in range(1, 101) if x % 2 == 0},
{x for x in range(1, 101) if x % 3 == 0},
{x for x in range(1, 101) if x % 5 == 0},
{x for x in range(1, 101) if x % 7 == 0}]
solutions = {}
for flag in product([0, 1], repeat=4):
possible_numbers = set(range(1, 101))
for index, value in enumerate(flag):
if value:
possible_numbers &= divisible_sets[index]
else:
possible_numbers -= divisible_sets[index]
if len(possible_numbers) == 1:
solutions[possible_numbers.pop()] = flag
correct_index = None
for answer in zip(*solutions.values()):
if sum(answer) == 1:
correct_index = answer.index(1)
for index, number in enumerate(solutions):
if index == correct_index:
return number>>> print(find_secret_number())
70Of course a fellow Mathematician, who could use their head and solve this problem easily, might consider this effort useless. Well the power of automated algorithmic computations is in scaling. What if for example we add more questions that could be heard and a bigger set of numbers? So, in order to challenge our fellow Mathematician let’s make this problem a bit harder: Say now for example instead of four questions we have seven questions, the set of numbers is between 1 - 10000 and the answer heard is “NO” instead of “YES”. The extra questions are the following:
Q5) Is the number divisible by nine?
Q6) Is the number divisible by twelve?
Q7) Is the number divisible by sixty-nine?
from itertools import product
from typing import Tuple
def check_combinations(numbers: Tuple,
max_number: int,
answer_heard: str) -> int:
divisible_sets = []
for divisor in sorted(numbers):
divisible_sets.append({x for x in range(1, max_number + 1)
if x % divisor == 0})
solutions = {}
for flag in product([0, 1], repeat=len(divisible_sets)):
possible_numbers = set(range(1, max_number + 1))
for index, value in enumerate(flag):
if value:
possible_numbers &= divisible_sets[index]
else:
possible_numbers -= divisible_sets[index]
if len(possible_numbers) == 1:
solutions[possible_numbers.pop()] = flag
correct_index = None
for answer in zip(*solutions.values()):
if answer_heard == 'NO':
answer = [0 if elem else 1 for elem in answer]
if sum(answer) == 1:
correct_index = answer.index(1)
for index, number in enumerate(solutions):
if index == correct_index:
return numberFirst check if it works with our initial example:
>>> print(check_combinations(numbers=(2, 3, 5, 7),
max_number=100,
answer_heard='YES'))
70It gives the same result as before. And if we revert the answer:
>>> print(check_combinations(numbers=(2, 3, 5, 7),
max_number=100,
answer_heard='NO'))
35>>> print(check_combinations(numbers=(2, 3, 5, 7, 9, 12, 69),
max_number=10000,
answer_heard='NO'))
5796Could any of the mathematicians find it in a reasonable amount of time? I doubt :)
We could even go further and use it to generate our own version of this puzzle with as many questions we want. We just need a unique secret number:
from random import sample
from typing import List, Tuple
def generate_questions_and_secret_number(
number_of_questions: int,
max_divisor: int,
max_number: int,
answer_heard: str)-> Tuple[List[int], int]:
while True:
questions = sample(range(2, max_divisor + 1),
number_of_questions)
secret_number = check_combinations(questions,
max_number,
answer_heard)
if secret_number:
return sorted(questions), secret_number>>> generate_questions_and_secret_number(number_of_questions=20,
max_divisor=100,
max_number=2000,
answer_heard='YES')
[3, 27, 36, 41, 42, 45, 49, 55, 57, 61, 69, 70, 71, 72, 74, 77,
80, 84, 90, 91]
1680This would correspond to the situation where Lucy would think a secret number between 1-2000, which is uniquely describable by the answer to the following 20 questions:
questions = [f"Is the number divisible by {x} ?" for x in
[3, 27, 36, 41, 42, 45, 49, 55, 57, 61, 69,
70, 71, 72, 74, 77, 80, 84, 90, 91]]>>> print(questions)
['Is the number divisible by 3 ?',
'Is the number divisible by 27 ?',
'Is the number divisible by 36 ?',
'Is the number divisible by 41 ?',
'Is the number divisible by 42 ?',
'Is the number divisible by 45 ?',
'Is the number divisible by 49 ?',
'Is the number divisible by 55 ?',
'Is the number divisible by 57 ?',
'Is the number divisible by 61 ?',
'Is the number divisible by 69 ?',
'Is the number divisible by 70 ?',
'Is the number divisible by 71 ?',
'Is the number divisible by 72 ?',
'Is the number divisible by 74 ?',
'Is the number divisible by 77 ?',
'Is the number divisible by 80 ?',
'Is the number divisible by 84 ?',
'Is the number divisible by 90 ?',
'Is the number divisible by 91 ?']