A movie connection quiz in Python

Not so long time ago, I was living and working in Graz, Austria, and in my free time, I would regularly take part in a Pub Quiz.

Every Tuesday evening, me and my team the legendary Dudes, would gather for more than four hours among 40 other teams in the Office Pub, hang on Nick’s the quizmaster words, competing with the other teams for the top 5 places that gave money prizes, and at the same time chasing the 500 euros special blockbuster round prize, which eventually led us arguing with the quizmaster about his notoriously tricky questions, that every time drove us mad.

This particular round was the highlight of the night. All the teams were dreaming of answering all ten questions correctly and hand them in within one minute to win the big prize. Moreover, you were given the first letter for every word in the answer as a hint. Sounds pretty easy right? But it was never that simple. The catch was that any wrong answer would cost you all the points and with that the chance of competing for the more humble top 5 prizes, which were still between 30 - 100 euros. The quizmaster was trying his best to lure us into risking with questions that appeared pretty obvious at first sight but in reality, they contained deadly traps. Most of the time you would hear desperate sighs as the last and more difficult answers were revealed, but once in a while, you would also hear screams of joy from the teams who achieved the ultimate feat, win the blockbuster.

It was a really fun experience and the whole event was like a cult night in Graz. You would find 400+ people trying to take a spot in the money, establishing rivals with other teams, and sometimes acknowledging the bests. You could not imagine the competition force, the religiously followed code of conduct of no cheating (no mobile phones, no cooperation between teams, no visits to the toilet during rounds), and the thrilling agony as you were approaching the final questions of the Blockbuster round and finding yourself one step of winning 500 euros and one step of losing all your points and chance of reaching the top places.

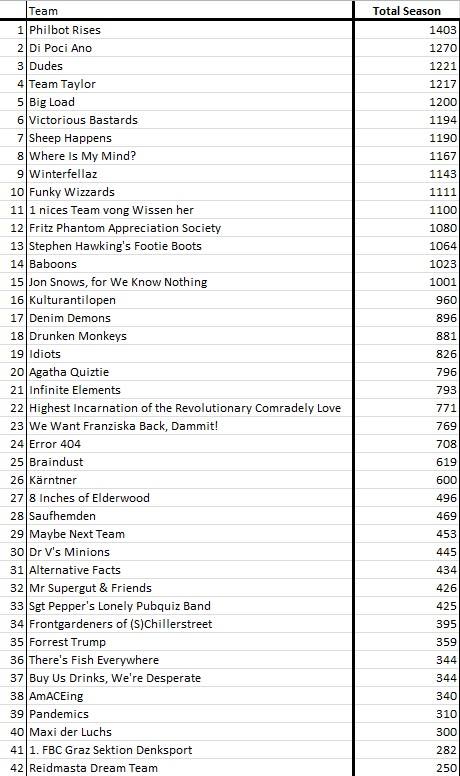
The Pub Quiz would climax at the end of May with the annual Play-Off rounds among the top-performing teams of the whole year and the final rankings with the yearly prizes. Here is an image of the top teams over the year 2018. As you can see we were 3rd it was quite a successful year :)

Every summer though, some teams would have a chance to host their own quiz. That is what we did one summer with great success. Below you can see a photo of me hosting the quiz :)

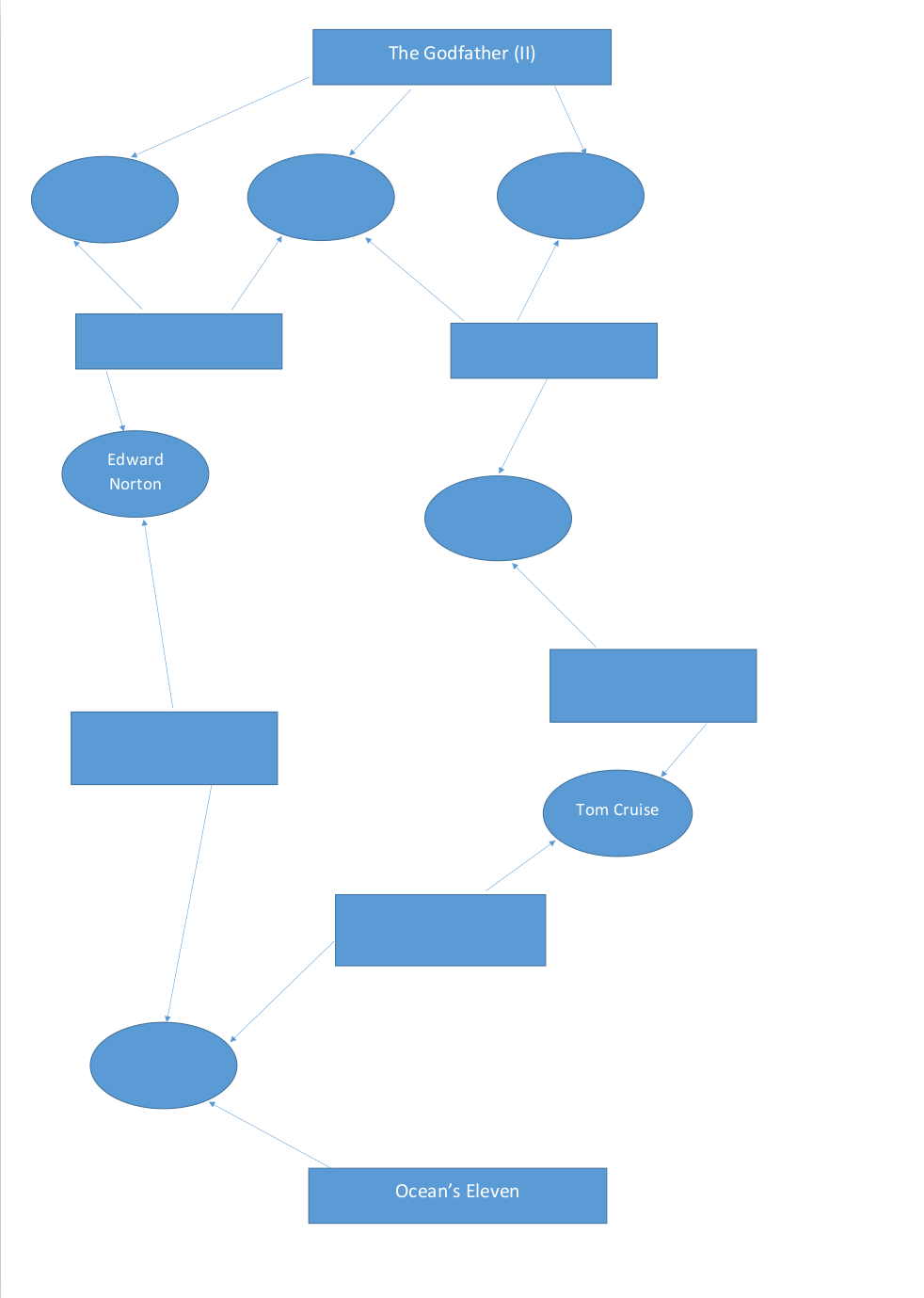
The whole process of coming up with a fun and challenging quiz took us days, if not weeks. In our quest to make something special, we came up with an idea of using a “movie connections” round. The idea was to construct a graph between movies and actors and guess the connecting movie(s) between two or more actors or the connecting actor(s) between two or more movies. After thinking and manually trying a lot of stuff we came up with the following quiz. Give it a try and see if you could solve it. There are two versions of it. The second version instead of a graph it contains a simple path but it has the added difficulty of including anagrams. For the record, only 2 teams out of 40 managed to solve it, so it was more difficult as we initially had thought.

Now it has been a while and I found myself reminiscing of the good old times there. By revisiting this quiz I also thought about how we could easily create such movie connections with … Python!

The first challenge we had to overcome back then was choosing a sweet spot between well-known movies and actors and not very obvious ones. There are endless possibilities which we could consider, but most of them are very hard even for movie experts. A good compromise would be to limit ourselves on IMDB’s top 250 movies list. This is a good mix between oldies and new movies, classics and blockbusters, Hollywood and international ones.

We are going to use IMDbPY which is a Python package for retrieving data from the IMDB movie database. Luckily for us in its latest edition, it features a function of retrieving the top 250 IMDB movie list. But let’s proceed step by step. First, let’s install the latest package version from the repository:

$ pip install git+https://github.com/alberanid/imdbpy

From here we can retrieve the top 250 movies:

from imdb import IMDb

# create an instance of the IMDb class
ia = IMDb()

top_movies = ia.get_top250_movies()

Let’s see which are the top 5 movies from the list. As of today, they are the following:

>>> top_movies[:5]

[<Movie id:0111161[http] title:_The Shawshank Redemption (1994)_>,
 <Movie id:0068646[http] title:_The Godfather (1972)_>,
 <Movie id:0071562[http] title:_The Godfather: Part II (1974)_>,
 <Movie id:0468569[http] title:_The Dark Knight (2008)_>,
 <Movie id:0050083[http] title:_12 Angry Men (1957)_>]

However, although the elements of this top_movies list are of type imdb.Movie.Movie, they do not contain all the information we will need, such as the complete movie cast. For that reason, we need to convert all incomplete Movie instances from this list to the complete ones, by using a call to function ia.get_movie. Since this might take some time it would be a good idea to install tqdm a smart Python progress bar meter.

$ pip install tqdm

from tqdm import tqdm

>>> top_250_movies = [ia.get_movie(top_movies[i].movieID) 
                      for i in tqdm(range(250))]
100%|██████████████████████████████████████████████████████| 
250/250 [09:19<00:00,  2.24s/it]

The operation above took almost ten minutes, so be patient! Now we have our top 250 Movie instances. The next task is more challenging. We would like to find actors that would appear in at least two movies from the list, to have at least one connection between two movies. But let’s first find a list of all the actors in the top 250 movies. Apparently in this list, we are going to have duplicates. Let’s count them and find the ones occurring the most.

from collections import Counter

actors = [actor['name'] for i in range(250) 
          for actor in top_250_movies[i]['cast']]
actors_freq = Counter(actors)
most_common_actors = actors_freq.most_common()

Great, it seems that’s all we need! Let’s print the top 10 most common actors:

>>> most_common_actors[:10]

[('Arnold Montey', 26),
 ('John Ratzenberger', 10),
 ('Sherry Lynn', 10),
 ('Bess Flowers', 10),
 ('Robert De Niro', 9),
 ('Mark Falvo', 9),
 ("William H. O'Brien", 9),
 ('Arthur Tovey', 8),
 ('Joseph Oliveira', 8),
 ('Mickie McGowan', 8)]

To be honest from this list I only know Robert de Niro. And wait a minute who is Arnold Montey, that had appeared in 26 top 250 movies of all time?! Well, I did search for him and apparently is an actor specialized in very small roles. He has appeared as a Stormtrooper in “Star Wars”, a stockbroker in “Inception”, an SS major in “Inglourious Basterds”, a Roman soldier in “Gladiator”, and a man selling cigarettes in “Gangs of New York”! Yet, he remains generally unknown to the public.

The lesson learned is that we need to include only “well-known” actors from this list. This is the subjective and manual part of the procedure. We need to consider the most popular actors that appeared at least in two movies from our list. Let’s first find out how many actors appear at least twice.

from itertools import takewhile
from operator import itemgetter

>>> sum(1 for _ in takewhile(lambda x: x >= 2, 
                             map(itemgetter(1), most_common_actors)))
1520

So, what I did next was to go through all those 1520 actors and choose the 150 most known actors according to myself. A more objective way would have been to use the “Star meter” feature of IMDB, but currently, it is only available in IMDB Pro version and not supported by the package we use. Here are the top 10 actors from my own assembled list along with the number of movies they had appeared from our list of top 250 movies. I hope you know all of them :)

('Robert De Niro', 9)
('Morgan Freeman', 7)
('Samuel L. Jackson', 7)
('Harrison Ford', 7)
('Christian Bale', 6)
('Michael Caine', 6)
('Tom Hanks', 6)
('Leonardo DiCaprio', 6)
('Charles Chaplin', 6)
('Al Pacino', 5)

I called this manually assembled list selected_actors. This list contains only the actors full names. If we want the real class instances we should do the following:

>>> actors_instances = [ia.get_person(
                        ia.search_person(
                        actors_to_select[i])[0].getID()) 
                        for i in tqdm(range(150))]
                       
100%|████████████████████████████████████████████████████████████████████
 150/150 [09:07<00:00,  3.65s/it]

What can also happen is that none of the actors we selected appear in some movies from the list. In other words, it is not guaranteed that the selected actors will span all the list of top 250 movies. Then some of the movies will be useless since they would be “isolated” nodes in the graph. Let’s find the movies that contain at least one actor from our list of selected actors. We are going to use a list comprehension again (perhaps you already noticed the trend of using list comprehensions in this article). This one is a bit more complicated but I find it elegant as only Python can be.

movies_to_select = [movie for movie in top_250_movies 
                    if any(actor in movie for actor in actors_instances)]

>>> len(movies_to_select)
173

So, we only need to consider 173 movies for building our graph. Let’s find their names:

movie_names = [movie['title'] for movie in movies_to_select]

Now comes the interesting part of constructing a graph to model relationships between actors and movies. Every node in the graph should either represent a movie or an actor and every edge in the graph would connect a movie with an actor that has appeared into it. For modeling such a graph and running some useful functions on it, we are going to use the well known NetworkX package. So, let’s install it:

$ pip install networkx

The first step is to create an undirected graph.

import networkx as nx

G = nx.Graph()

Then let’s compute the edges of the graph. There can only be an edge between a movie and an actor if the actor appeared in the movie. There are two different methods to compute the edges.

First method:

edges = []
for i in tqdm(range(173)):
    movie = ia.get_movie(movies_to_select[i].movieID)
    movie_name = movie['title']
    for actor in movie['cast']:
        actor_name = actor['name']
        if actor in actors_to_select:            
            edges.append((movie_name, actor_name))

Second method:

edges_alt = [(movie_names[i], actors_to_select[j]) 
             for i, movie in enumerate(movies_to_select) 
             for j, actor in enumerate(actors_instances) 
             if actor in movie]

The second method looks simpler and more straightforward. There is though a slight caveat. The second method produces ten additional edges for the graph. These are the following:

>>> set(edges_alt) - set(edges)
{('Aladdin', 'Peter Lorre'),
 ('Dial M for Murder', 'Alfred Hitchcock'),
 ('Into the Wild', 'Jack Nicholson'),
 ('Joker', 'Bradley Cooper'),
 ('Kill Bill: Vol. 1', 'Charles Bronson'),
 ('Kill Bill: Vol. 1', 'Quentin Tarantino'),
 ('La Haine', 'Jodie Foster'),
 ('Pulp Fiction', 'Danny DeVito'),
 ('Requiem for a Dream', 'Robert Redford'),
 ('The Departed', 'Brad Pitt')}

That looks weird… Jodie Foster in the French film ‘La Haine’ and Danny DeVito in Pulp Fiction certainly does not seem right. But if we have a closer look in the documentation here is what it says about the predicate actor in movie:

“The in operator can be used to check whether a person worked in a given movie or not” The key word here is worked. And let’s see why:

For “La Haine” the Blu-ray release included an introduction by actor Jodie Foster and for “Pulp Fiction” Danny DeVito served as Executive Producer on the film. But these types of relations should not be added as edges in our graph. We are not interested in actors who have worked in a movie in different roles than acting. Therefore, we need to check explicitly if an actor appeared in movie[‘cast’]. Unfortunately the predicate if actor in movie[‘cast’] does not seem to work properly. But there is a workaround to it:

edges_alt_2 = [(str(movie), actor) 
               for movie in movies_to_select 
               for actor in actors_to_select 
               if actor in str(movie['cast'])]

And as you see we get the exact same edges as with the first method.

>> len(edges_alt_2)
449
>> set(edges) == set(edges_alt_2)
True

After applying the correct method we also need to check whether there is a movie or an actor that is left with no connections at all (isolated node). In that case, we would have to disregard them.

from itertools import chain

>>> set(movie_names + actors_to_select) - set(chain(*edges))
{'La Haine'}

As expected since Jodie Foster is no longer affiliated with the film, we need to discard it. Sorry for the French audience, I have seen the movie and I can definitely recommend it :) It might also be that with this new rule we might need to remove actors that play only in one movie. Let’s check:

all_freqs = Counter(list(chain(*edges)))
alone_actors = [node for node, freq in all_freqs.items() 
                if freq < 2 and node in actors_to_select]

>>> alone_actors
['Tim Robbins', 'Rita Hayworth']

Although there is a subtle connection based on a famous movie from our list “The Shawshank Redemption” we, unfortunately, need to remove them both.

movie_names.remove('La Haine')

for lonely_actor in alone_actors:
    actors_to_select.remove(lonely_actor)

edges_to_remove = [edge for edge in edges 
                   if alone_actors[0] in edge 
                   or alone_actors[1] in edge]

for edge in edges_to_remove:
    edges.remove(edge)

Now we can finally add the nodes and the edges to the graph:

# Add the top 172 movies and the top 148 actors we manually selected
G.add_nodes_from(movie_names + actors_to_select)

# Add the 447 edges of the graph
G.add_edges_from(edges)

Now that we have modeled the relations into a graph we can get quite some interesting insights. One of them is to find the nodes which have the most neighbors.

most_connected_nodes = sorted(G.degree, 
                              key=itemgetter(1), 
                              reverse=True)

>>> most_connected_nodes[:10]
[('Avengers: Endgame', 15),
 ('Avengers: Infinity War', 13),
 ('The Lord of the Rings: The Return of the King', 10),
 ('The Lord of the Rings: The Fellowship of the Ring', 10),
 ('The Lord of the Rings: The Two Towers', 9),
 ('The Dark Knight Rises', 9),
 ('Robert De Niro', 9),
 ('The Godfather: Part II', 8),
 ('Pulp Fiction', 8),
 ('Cinema Paradiso', 8)]

Both the Avengers movies gather a surprising amount of superstar actors from our list.

What we could find next is the number of connected components in our graph. Ideally, we should have one big connected component, meaning we can always find a path from one movie to another in our list. But is this the case? Let’s find out:

components = list(nx.connected_components(G))

>>> print("Connected components sizes:", list(map(len, components)))
Connected components sizes: [262, 5, 40, 4, 3, 3, 3]

So, we have one very large component, where the majority of our nodes is located, and one of a smaller size. Then we have a few very small components. Let’s see what they contain:

>>> components[1]
{'High and Low', 
 'Rashomon', 
 'Seven Samurai', 
 'Toshirô Mifune', 
 'Yojimbo'}

>>> components[3]
{'Arnold Schwarzenegger',
 'Linda Hamilton',
 'Terminator 2: Judgment Day',
 'The Terminator'}
 
>>> components[4]
{'Citizen Kane', 'Orson Welles', 'The Third Man'}

>>> components[5]
{'John Cleese',
 'Monty Python and the Holy Grail',
 "Monty Python's Life of Brian"}

>>> components[6]
{'Hacksaw Ridge', 'Into the Wild', 'Vince Vaughn'}

So, we have an “Akira Kurosawa” component, a “Terminator” series component, an “Orson Welles” component, a “Monty Python” component, and a “Vince Vaughn” component. Since all of them are very small we can disregard them. Then we are left with only two interesting components. Let’s look closer at a few random nodes from the smaller one:

import random

>>> list(random.sample(components[2], 10))
['Clark Gable',
 'Cinema Paradiso',
 'The Gold Rush',
 'Kirk Douglas',
 'The Great Dictator',
 'Charles Chaplin',
 'Marlene Dietrich',
 'Rear Window',
 'Witness for the Prosecution',
 'Vertigo']

Well, it seems that the smaller components consist mostly of oldies and classics, while the bigger component mostly of modern movies. This can be interesting because we are going to generate different quizzes per component.

But first let’s remove all redundant nodes from the graph:

# Keep only nodes from components 0 and 2
for index in [1, 3, 4, 5, 6]:
    for node in components[index]:
        G.remove_node(node)

# Compute separately the movies and actors from each component
movies_1 = [elem for elem in components[0] if elem in movie_names]
movies_2 = [elem for elem in components[1] if elem in movie_names]
actors_1 = [elem for elem in components[0] if elem in actors_to_select]
actors_2 = [elem for elem in components[1] if elem in actors_to_select]
        
components = list(nx.connected_components(G))

And let’s validate that now we are left with only two components:

>>> print("Connected components sizes:", list(map(len, components)))
Connected components sizes: [262, 40]

Now it is easy to construct quizzes of the second type that include anagrams, as the one we showed in the beginning. Let’s first concentrate on the second component. It has 15 actors and 25 movies. Let’s find the longest path in this graph. Generally this is a difficult NP-Hard problem but in this small case it can be solved easily:

max_path_len = 0
max_path = None
for idx, source in enumerate(actors_2):
    for target in actors_2[idx + 1:]:
        # Compute all paths between source and target
        all_paths = list(nx.all_simple_paths(G, source, target))
        # Found no path between source and target
        if not all_paths:
            continue
        # Compute all paths lengths between source and target
        all_paths_lengths = list(map(len, all_paths))
        # Compute the maximum length
        max_length = max(all_paths_lengths)
        max_index = all_paths_lengths.index(max_length)
        # Update the maximum length found so far, if needed
        if max_length > max_path_len:
            max_path_len = max_length
            max_path = all_paths[max_index]

>>> max_path_len
11

Now we can go on and create some nice anagrams. We are going to use for that purpose the Internet Anagram Server. Here is a cool quiz we can generate. You need first to solve all the anagrams which represent actors from some old movies and then you need to find the connecting movie between each pair of actors!

anagrammed_actor_names = ["Scary Percent", 
                          "Tag Ran Cry", 
                          "Teach Child Frock", 
                          "Teamster Jaws", 
                          "Lake Clergy"]

print(f"0) {max_path[0]} (actor)")
for idx, elem in enumerate(max_path[1:]):
    if idx % 2 == 0:
        print(f'{idx + 1}) .......... (movie) ..........')
    else:
        print(f'{idx + 1}) {anagrammed_actor_names[idx//2]} (actor)')

0) Clotilde Mollet (actor)
1) .......... (movie) ..........
2) Scary Percent (actor)
3) .......... (movie) ..........
4) Tag Ran Cry (actor)
5) .......... (movie) ..........
6) Teach Child Frock (actor)
7) .......... (movie) ..........
8) Teamster Jaws (actor)
9) .......... (movie) ..........
10) Lake Clergy (actor)

If we are going to use the first component, which is larger, we can have many more solutions. Here is a method of producing many of them. We choose randomly a source (an actor to start with) and a target (an actor to finish). Then we generate all possible paths between them and up to a given length and stop only when we find a path of length 21. A path of such length will guarantee we have 10 anagrammed actor names and 10 connecting movies to solve.

all_paths_gen = nx.all_simple_paths(G, 
                                    source=random.choice(actors_1), 
                                    target=random.choice(actors_1), 
                                    cutoff=21)
                                    
while True:
    path = next(all_paths_gen)
    if len(path) == 21:
        break

Here is a quiz I generated using this method: Again you must first solve the actor anagrams and then find the connecting movies between them! Questions 1-10 are the connecting movies and the anagrams in between represent the actors.

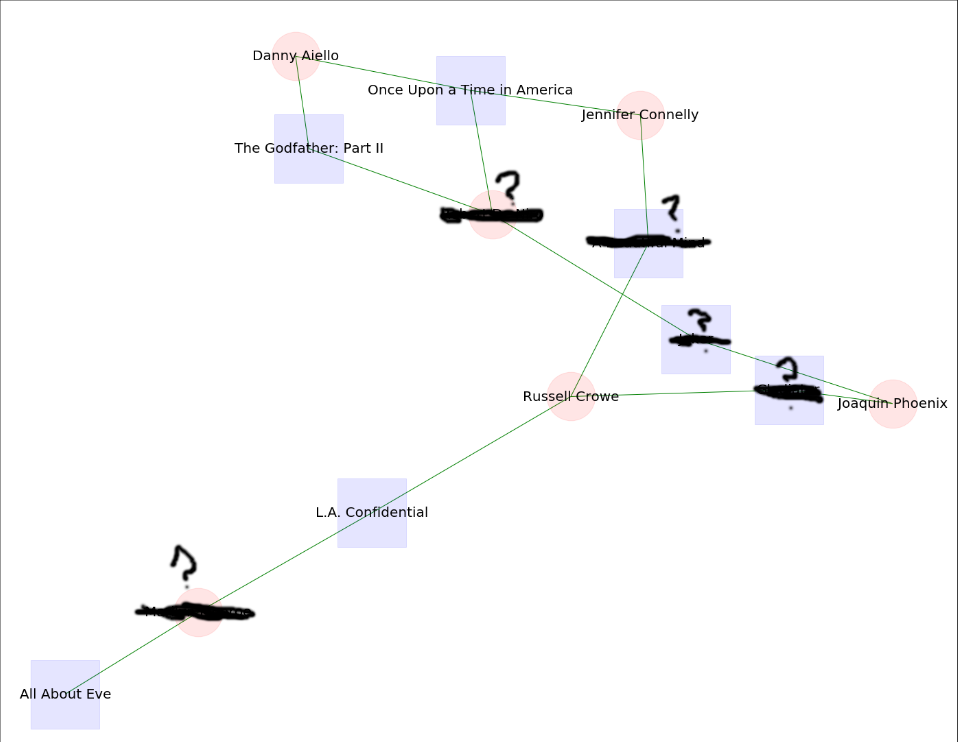
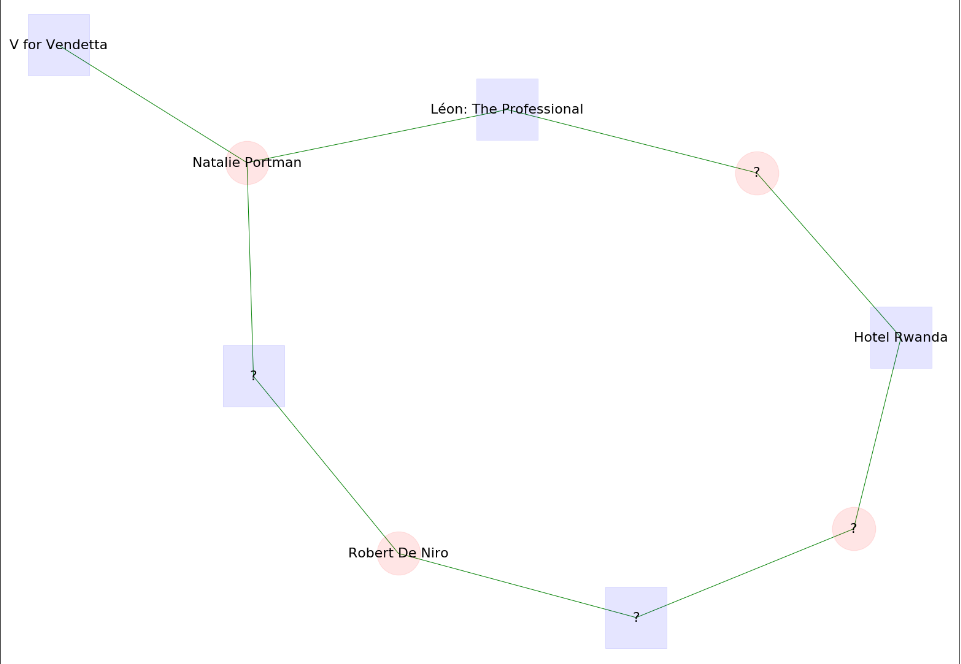
Creating quizzes like the first one we presented at the beginning of the post, that contains a connection graph instead of a path, is a bit more challenging.

• We need to find a fairly simple but not too simple (e.g. a single path) connection graph between two movies.
• All the path lengths between the source (start movie) and the target (end movie) should not be larger than a certain number, otherwise it makes it very complicated to solve.
• There should be no more than 20 nodes, also for the sake of simplicity.

We can use the built-in function networkx.all_simple_paths, which finds all paths in a graph between two nodes up to a certain length.

The problem is that if this function cannot find such paths will keep searching for a very long time.

In this case, we may want to put a timeout, terminate the search, and consider a different pair of nodes to search for paths between them.

To implement a timeout method for our function, we are going to use Process from multiprocessing module. We are going to set a reasonable timeout of 5 seconds.

Moreover, to be able to access the return value of the function, we need to have a shared variable. For that purpose, we are going to use a dictionary provided by multiprocessing.Manager.

Therefore, as a target argument in Process call, where we need to put the function, we cannot simply use the networkx.all_simple_paths. Instead, we need to wrap it into another function, that we call find_all_paths, which contains the shared dict variable.

def find_all_paths(G, start, end, depth, return_dict):
    value = nx.all_simple_paths(G, start, end, depth)
    return_dict[0] = list(value)

from multiprocessing import Manager, Process
from typing import List, NamedTuple


class Connections(NamedTuple):
    start_movie: str
    end_movie: str
    max_length: int
    paths: List[List]


def find_paths_random(max_depth: int = 8) -> Connections:
    """ Method to randomly pick two movies in the graph and find 
    all paths between them up to a certain length

    :param max_depth:
        The maximum path length between the two movies
    :return:
        A NamedTuple containing the start movie, the end movie, 
        the maximum path length, and a list of all paths between 
        the two movies.
    """

    while True:
        start_movie, end_movie = tuple(random.sample(movies_1, 2))
        print(start_movie, end_movie)

        manager = Manager()
        return_dict = manager.dict()
        action_process = Process(
            target=find_all_paths,
            args=(G, start_movie, end_movie, max_depth, return_dict))
        action_process.start()
        action_process.join(timeout=5)
        action_process.terminate()
        solutions = return_dict.values()[0]

        # If there was a timeout solutions will be an empty list
        # Otherwise, we need to choose a pair of movies again.
        if solutions:
            break

    return Connections(start_movie, end_movie, max_depth, solutions)

def construct_graph(paths: List[List]) -> nx.Graph:
    """ Method to construct the connection graph given a list of all 
    paths between the start node (source) and the end node (sink)

    :param paths:
        A list of paths between the start node and the end node
    :return:
        A graph with all the nodes and edges between the start node
        and the end node
    """
    g = nx.Graph()
    new_nodes = set()
    new_edges = set()
    for elem in paths:
        new_edges |= set(zip(elem, elem[1:]))
        new_nodes |= set(elem) 
    g.add_nodes_from(new_nodes)
    g.add_edges_from(new_edges)
    return g

Sometimes we might end up with a long and complicated graph. It makes sense then to have a limit on the number of nodes the graph can have. For that purpose, we need a second function that will disregard some paths if the number of nodes is already above a certain number.

def smaller_graph(paths: List[List], max_nodes: int = 20) -> nx.Graph:
    """ Method to construct the connection graph given a list of all 
    paths between the start node (source) and the end node (sink), 
    with the restriction that we should have a maximum number of nodes 
    in the graph

    :param paths:
        A list of paths between the start node and the end node
    :param max_nodes:
        The maximum number of nodes we can have in the graph
    :return:
        A graph with all the nodes and edges between and including
        start and end node
    """

    g = nx.Graph()
    while True:
        new_nodes = set()
        new_edges = set()
        for elem in paths:
            new_edges |= set(zip(elem, elem[1:]))
            new_nodes |= set(elem)
        # When we reach our limit exit the loop
        if len(new_nodes) < max_nodes:
            break
        # As long as we keep having more nodes than our limit we
        # need to drop the last path. This will create less nodes
        # in the next iteration until we reach our limit
        paths = paths[:-1]

    g.add_nodes_from(new_nodes)
    g.add_edges_from(new_edges)
    return g

The following lines of code put them altogether and construct the graph

connections = find_paths_random()
g = smaller_graph(connections.paths)

nodes_movies = [elem for elem in g.nodes() if elem in movies_1]
nodes_actors = [elem for elem in g.nodes() if elem in actors_1]

Now, we come to the last part where we need to visualize the graphs and “hide” some intermediate nodes. We show how this can be done below.

import matplotlib.pyplot as plt

# Make a slightly bigger figure to visualize the graph better
figure = plt.figure(figsize=(25, 20))

# Get all the graph nodes and edges
edges = list(g.edges())
nodes = list(g.nodes())

# Set positions for all nodes
pos = nx.spring_layout(g) 

# Draw the movie nodes as blue squares
nx.draw_networkx_nodes(g,
                       pos,
                       nodelist=nodes_movies,
                       node_shape="s",
                       node_color='b',
                       alpha=0.1,
                       node_size=10000)

# Draw the actor nodes as red circles
nx.draw_networkx_nodes(g,
                       pos,
                       nodelist=nodes_actors,
                       node_color='r',
                       node_shape="o",
                       alpha=0.1,
                       node_size=5000)

# Draw the edges as green
nx.draw_networkx_edges(g,
                       pos,
                       edgelist=edges,
                       edge_color='g')

# Get the labels of the start and the end nodes 
start_end_nodes = [connections.start_movie, connections.end_movie]
labels1 = {elem: elem for elem in start_end_nodes} 

# Get the labels for all the nodes in between. 
labels2 = {elem: elem for idx, elem in enumerate(nodes) 
           if elem not in start_end_nodes}

# Get the labels of the solutions (all visible)
labels_solutions = {elem: elem for elem in nodes}

# Randomly choose half of the intermediate nodes as "secret nodes" 
# and show them as "?"
void = random.sample(labels2.keys(), len(labels2) // 2)
for elem in void:
    labels2[elem] = "?"

# Update all the labeled nodes    
labels1.update(labels2)

# Draw the labels of the graph
nx.draw_networkx_labels(g, pos, labels1, font_size=18)

Now we can create as many quizzes as we want! Have a look at the following ones that are created with the code above and give them a try. Let’s start with some fairly easy ones and move to some harder ones. To see the pictures better try to right-click on them and choose the “Open image in new tab” option.

Some easy ones to start:

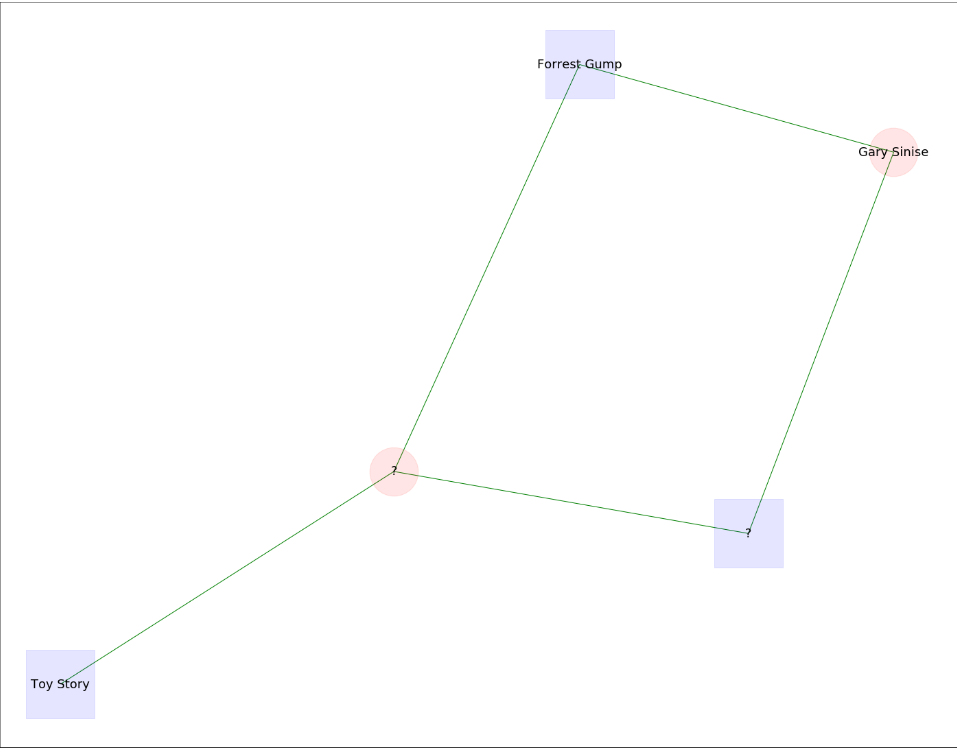
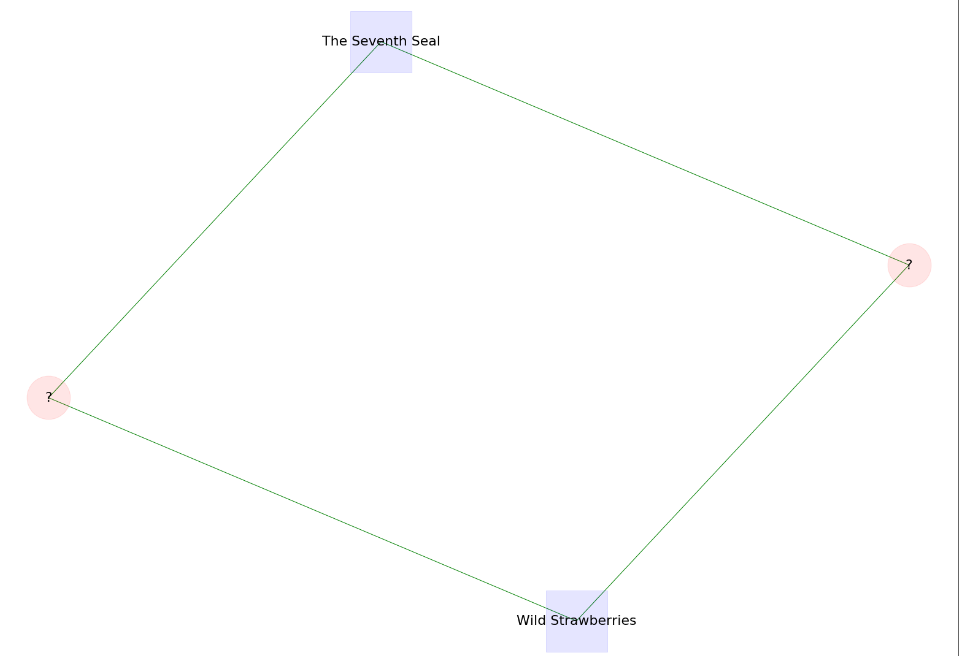
Some medium difficulty ones:

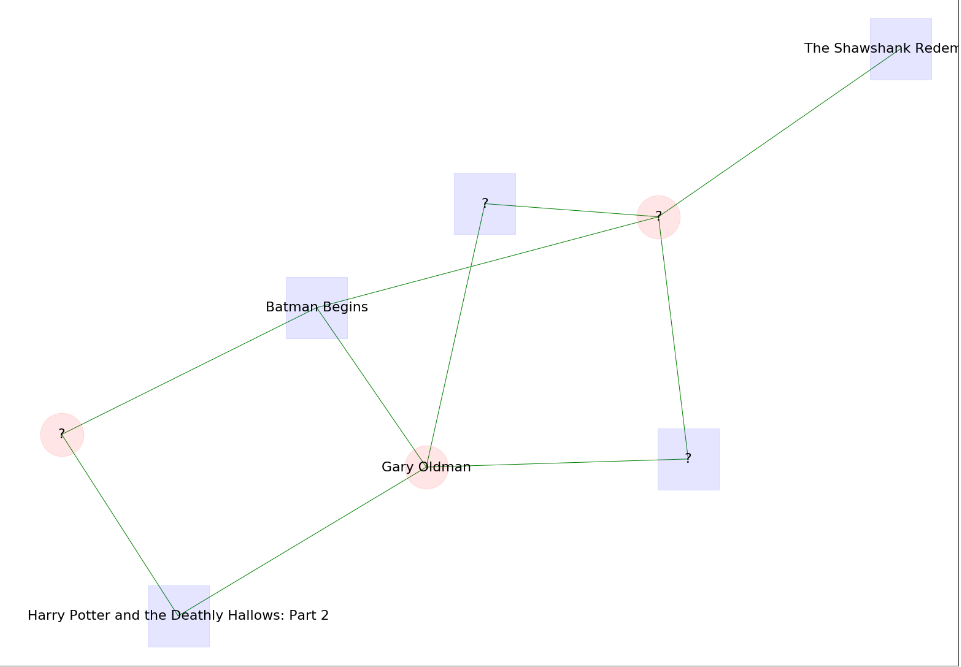
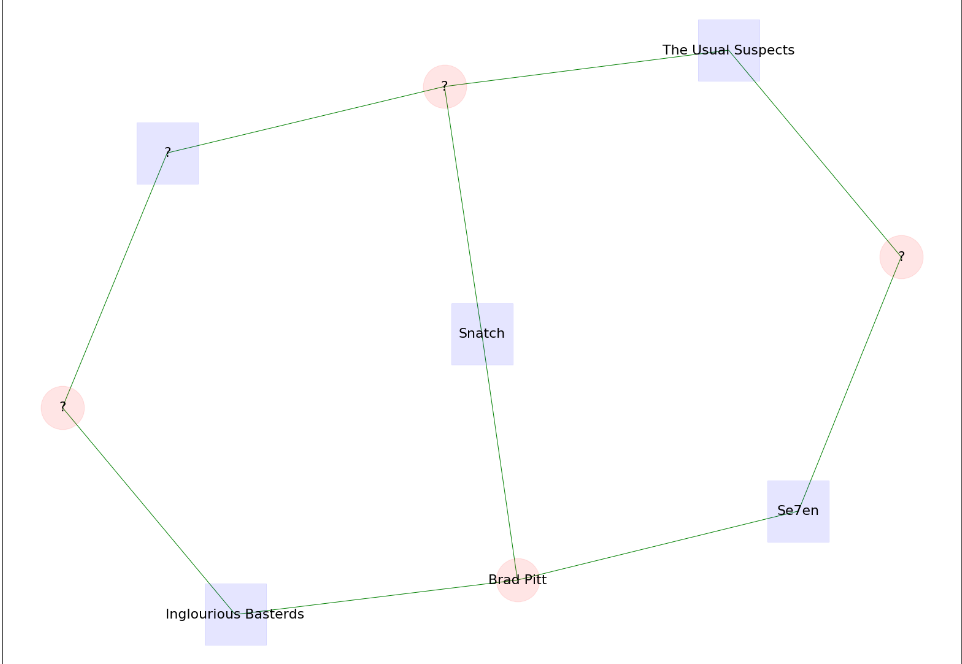
Finally, here are some hard ones!

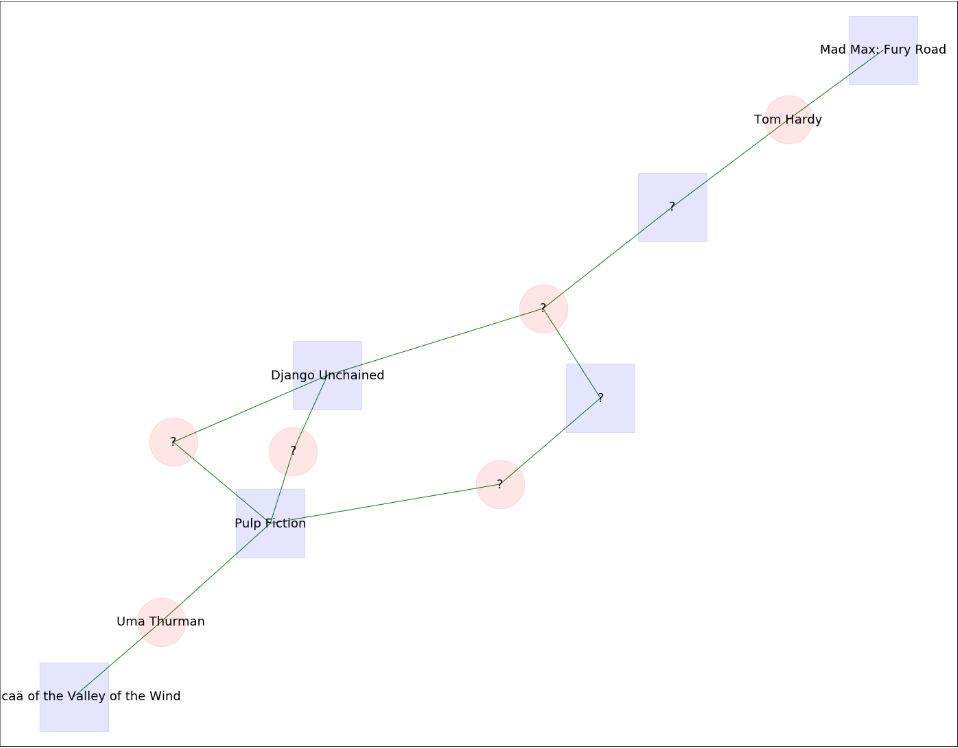
In the next blog post, I am going to provide the solutions to all the quizzes presented here. Also in a future blog post, I am going to try and make a Python app that would generate such quizzes using Pythonista!

References:

An article about the Graz Pub Quiz in the local newspaper (in German)