POSTS
Avoid using an empty list as a default argument to a function
A very common error in Python is the use of an empty list as a default argument to a function. This is not the right way to do it and can cause unwanted behavior. See for example below:
def append_to_list(element, list_to_append=[]):
list_to_append.append(element)
return list_to_append>>> a = append_to_list(10)
[10]
>>> b = append_to_list(20)
[10, 20]This is not the behavior we wanted! A new list is created once when the function is defined, and the same list is used in each successive call. Python’s default arguments are evaluated once when the function is defined, not each time the function is called.
See for example the code visualization for the above code:
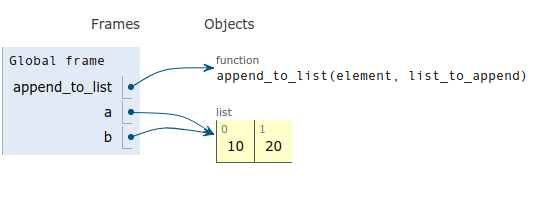
The solution and the standard way of doing it right is to pass to a Python function as a default argument None instead of [].
def append_to_list(element, list_to_append=None):
if list_to_append is None:
list_to_append = []
list_to_append.append(element)
return list_to_append>>> a = append_to_list(10)
[10]
>>> b = append_to_list(20)
[20]See now how the correct code visualization looks like:
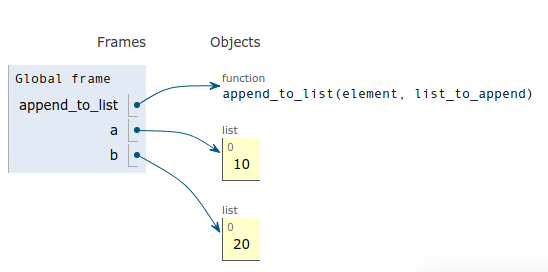
Many who are new to Python tend to find this as a shortcoming of the language. On the contrary, it is not a bug but a valid language feature instead.
This behavior, that might shock newcomers to Python, can be easily explained if you think of functions in Python as objects. After all everything in Python is an object, right? An object is evaluated upon definition. The same happens to functions when the default parameters take their values upon the function definition with def. Upon calling an object multiple times the state of its member variables may change. Similarly, upon calling a function many times the state of its default parameters may change. This can be seen below, where we check the default arguments of a function after every successive call:
def append_to_list(element, list_to_append=[]):
list_to_append.append(element)
return list_to_append>>> append_to_list.__defaults__
([],)
>>> a = append_to_list(10)
>>> a = append_to_list(10)
>>> a = append_to_list(10)
>>> append_to_list.__defaults__
([10, 10, 10],)As we showed we should generally avoid having mutable default arguments to functions.However, this could sometimes be used for our benefit. There is a technique called memoization, where we store previous values of computed values instead of using an expensive computation every time from the scratch. This technique proves quite useful especially when it is combined with recursion. See a classic example of it, the fibonacci numbers, where we use a mutable default argument to speed up the computation:
First here is the classic recursive version of computing the Fibonacci numbers, which proves to be very costly.
def fibonacci_classic(value):
if value == 0 or value == 1:
return value
else:
return fibonacci_classic(value - 1) + fibonacci_classic(value - 2)>>> %time fibonacci_classic(40)
CPU times: user 34.5 s, sys: 0 ns, total: 34.5 sIt took 34 seconds, which was a lot! The reason is that if we look at the recursion tree for computing the fibonacci number n, it has a depth of n as well. So that gives us an exponential time complexity of O(2^n). Actually it has a tight bound of O(1.61^n).
Interesting fact: Fib(n) / Fib(n - 1) equals the golden ratio, which is around 1.61 as well!
In order to think how we could optimize this, take a look at the recursion tree below for computing the fifth fibonacci number.
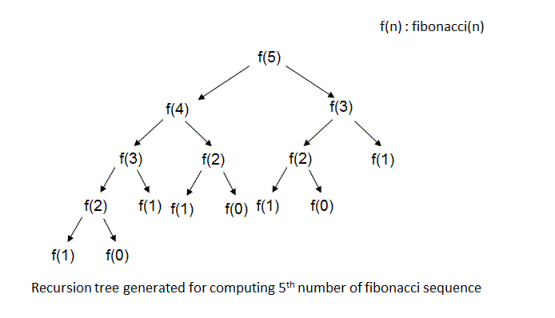
In order to compute f(5) we need to compute f(4) and f(3). But f(3) is already computed when we computed f(4). So, we would need to find a way to add “state” to our function calls so that we would remember already computed values.
So, what if we stored the already computed Fibonacci values in a dictionary that we could then pass it as default argument to a function? A dict is a mutable type in Python ensuring that it will be the same on every function call. This time we used mutability to our advantage!
def fibonacci(value, memo={0: 0, 1: 1}):
try:
fib = memo[value]
except KeyError:
fib = fibonacci(value - 1, memo) + fibonacci(value - 2, memo)
memo[value] = fib
return fib>>> %time fibonacci(40)
CPU times: user 32 µs, sys: 0 ns, total: 32 µsIt is a million times faster!
Actually if we omit the try..except and use “Look before you leap”(LBYL) instead of EAFP(“it’s easier to ask for forgiveness than permission”) we get even faster results:
def fibonacci_lbyl(value, memo={0: 0, 1: 1}):
if value in memo:
return memo[value]
else:
fib = fibonacci_lbyl(value - 1, memo) + fibonacci_lbyl(value - 2, memo)
memo[value] = fib
return fib>>> %time fibonacci_lbyl(40)
CPU times: user 17 µs, sys: 0 ns, total: 17 µsAnother option would be to use function attributes instead of default arguments:
def fibonacci_attr(value):
if value in fibonacci_attr.memo:
return fibonacci.memo[value]
else:
fib = fibonacci_attr(value - 1) + fibonacci_attr(value - 2)
fibonacci_attr.memo[value] = fib
return fib
fibonacci_attr.memo = {0: 0, 1: 1}We could also implement this by making our own memoized function decorator:
def memoize(function_to_decorate, memo={}):
def memoized(value):
if value in memo:
return memo[value]
else:
result = function_to_decorate(value)
memo[value] = result
return result
return memoized
@memoize
def fibonacci_memo(value):
if value == 0:
return 0
elif value == 1:
return 1
else:
return fibonacci_memo(value - 1) + fibonacci_memo(value - 2)Here is an important remark. Would we have the same effect if we did not apply @memoize to fibonacci_memo and just called memoize(fibonacci_memo)(value) instead? Let’s see:
>>> %time memoize(fibonacci_memo)(40)
CPU times: user 33.2 s, sys: 3.99 ms, total: 33.2 s
>>> %time memoize(fibonacci_memo)(40)
CPU times: user 4 µs, sys: 0 ns, total: 4 µs
>>> %time memoize(fibonacci_memo)(39)
CPU times: user 20 s, sys: 6.02 ms, total: 20 sAs you can see it’s a big difference from using it as a decorator. The difference is that fibonacci_memo does not change. This means that memoization only affects the external call with argument 40, all subsequent calls are unmemoized, because they call the fibonacci_memo plain without memoization. But if you use it as a decorator then recursive calls are memorized and you’ll get speedup even with cold cache!
Let’s try to apply our decorator to another recursive problem that would welcome a memoization speedup namely the computation of the factorial of a value.
@memoize
def factorial(n):
if n == 0 or n == 1:
return 1
else:
return factorial(n - 1) * n>>> factorial(5)
5What went wrong?! The output should have been 120 and not 5. The problem is that the way we defined the memoize decorator we have a global cache. So by memoizing factorial we get results from fibonacci! This is another side effect of using a mutable default argument. If we would like to avoid that we should rewrite our memoize decorator. We should also use the functools.wraps in order not to lose some important information about the decorated function such as name, docstring, args.
from functools import wraps
def memoize(function_to_decorate):
memo = {}
@wraps(function_to_decorate)
def memoized(value):
if value in memo:
return memo[value]
else:
result = function_to_decorate(value)
memo[value] = result
return result
return memoized>>> fibonacci_memo(5)
5
>>> factorial(5)
120What if we used the Python’s standard library implementation of memoization? For that reason there is functools.lru_cache decorator that we can use for this purpose. For you that are familiar with algorithms what we achieve this way is applying a dynamic programming technique to the original problem. We break it into subproblems which are computed only once and we store in cache the solution for them, in order to be used next time.
from functools import lru_cache
@lru_cache(maxsize=128)
def fibonacci_cache(value):
if value == 0 or value == 1:
return value
else:
return fibonacci_cache(value - 1) + fibonacci_cache(value - 2)So finally some time comparisons between these two techniques:
>>> %time fibonacci(800)
CPU times: user 2.24 ms, sys: 0 ns, total: 2.24 ms
>>> %time fibonacci_lbyl(800)
CPU times: user 778 µs, sys: 27 µs, total: 805 µs
>>> %time fibonacci_memo(800)
CPU times: user 1.55 ms, sys: 55 µs, total: 1.61 ms
%time fibonacci_cache(800)
CPU times: user 1.01 ms, sys: 36 µs, total: 1.05 msBoth the lru_cache decorator and the fibonacci_lbyl proved to be two to three times faster compared to our memoization and our custom memoized decorator.
Moral of the story: Do not reinvent the wheel and prefer Python standard’s library methods!
However, there is one interesting fact. All of the methods but one tend to fail by reaching maximum resursion depth with results above 800. There is one method though that gives us results up to 2500 and very fast as well! Can you guess which is this method?
>>> %time fibonacci_????(2500)
CPU times: user 2.02 ms, sys: 41 µs, total: 2.06 ms
Wall time: 2.06 ms
13170905167519496295227630871253164120666069649925071418877469367275308
70405038425764503130123186407746570862185871925952766836352119119528156
31558263246079038383460565488061265771846563256883924597824847305817942
20707355531247163854508866405523922738567706722397971642643569276613083
49671941673643205733343592701716715788255170679575500279186053316365583
25918692735935102338729837168622286082741537144355375995365951412088276
38081425933664024722513483600089155852152915049843716975238711995539357
14056959634778700594751875To summarize here is a Tweet from one of my favorite Twitter accounts on the web the one of Raymond Hettinger’s.
#python tip: Don't use mutable default arguments
— Raymond Hettinger (@raymondh) March 12, 2015
def wrong(x, s=[]):
...
def right(x, s=None):
if s is None:
s = []
...
Quiz:
Why don’t you want to test your knowledge and try this small quiz, that I created? Take Quiz!
References: